“文丘里面罩是根据文丘里原理制成”,当你在中文互联网搜索文丘里面罩时大约会首先看到这样一句话。“流速越快,压力越低”,这是被广泛接受的对于文丘里效应的解读。1960年,EJ Moran Campbell博士在《柳叶刀》杂志发文,首次描述了一种能够卷吸空气从而提供可控氧气浓度的氧疗装置,并称其为文丘里面罩(Venturi mask)[1]。显然,Campbell博士认为该装置应用了文丘里效应,并且70多年来,这种观点被大量专业论文和教材认同并引用。然而,“从来如此,便对么?”
图片来源于网络
早在40多年前,即有学者明确指出,文丘里面罩使用的不是文丘里或伯努利原理[2,3]。现在很多专业的呼吸治疗教材也都对此做出了澄清,但大都寥寥数笔、语焉不详,使读者云里雾里。因此,本文试图阐释什么是真正的文丘里效应以及文丘里面罩到底应用了什么样的原理。伯努利原理(Bernoulli's principle)指出,流体速度的增加与压力的减小或流体势能的减小同时发生(图1)。该原理以瑞士数学家丹尼尔·伯努利(Daniel Bernoulli)的名字命名,他于1738年在其著作《流体力学》(Hydrodynamics)中发表了该原理。用公式表示为:公式中,v为流线上某点流体的速度,g为重力加速度,z为参考平面上方该点的高度,p为该点的压力,ρ为流体的密度。该式即为伯努利方程。伯努利原理的本质即为流体中的机械能守恒定律,即流体的动能、重力势能和压力势能的总和保持不变。但因伯努利原理的提出时间早于机械能守恒定律一百多年,因此其地位显得十分重要。伯努利原理也可以用牛顿第二定律解释[4]。在图2所示的例子中,高度无变化,gz项可以省去,将伯努利方程稍加变形可得:根据连续性方程可知,单位时间内经过截面A1和A2的流量必然相同,由于A1>A2,则v1<v2。假如我们在管道中放一个轻质小球,那么小球在从1点运动到2点的过程中,其速度必然随水流越来越快。根据牛顿第二定律,力是改变物体运动状态的原因,因此在这段路程中,小球必然受到一个向前的力。
图2 文丘里效应
这个力显然是流水作用产生的。请注意,由于小球与水流保持相对静止,它所受的力全部来自水的静压力,而不包括水流的曳力以及其他的动力学力。由于小球受到的净力向前,则必有其后部的压力大于前部的压力,即流速快的地方压力低。然而,伯努利原理并非一个普遍适用的定律,它的适用条件其实非常苛刻:(4)同一条流线:也就是说,压力的比较必须在同一条流线上才有意义。因此,对于图2所示过程,伯努利原理的完整表述应为:对定常流的不可压缩的无粘流体,在同一条流线上,速度快的地方压力低。而且,需要注意的是,伯努利原理说的流速快总是伴随着压力低,是一种“相关性”描述,而不是流速快导致压力低这样的“因果性”描述。文丘里效应(Venturi effect)由意大利物理学家乔瓦尼·巴蒂斯塔·文丘里(Giovanni Battista Venturi)于1797年发表,专指流体通过管道的狭窄区域时,速度会增加,而其静压会降低(图2),依据此效应发明了文丘里管等诸多实用装置。文丘里效应可以用伯努利原理解释,二者本质上并无不同。文丘里面罩是一种能够提供稳定和可控氧浓度的氧疗装置,最初是为解决慢性呼吸疾病患者吸入高浓度氧气纠正低氧但容易出现二氧化碳潴留的问题而设计。在此之前,解决方法是间歇性氧疗,Moran将其形容为将溺水者救出水面,然后又将他推向更深的深渊[1]。文丘里面罩的发明有效地解决了这一问题。当一定流量的加压气体(通常是氧气)通过文丘里面罩的喷嘴时,其周围的空气会被卷吸(entrainment)进主气流中,从而实现气体总流量的增加和氧浓度的下降。因此,高流量和高浓度不可兼得,只有在低浓度下才是真正的高流量装置。如果一味提高氧浓度,将使得输出总流量降至低于患者的吸气流量,出现空气稀释,导致FiO2不稳定。空气卷吸的量取决于喷嘴口径的大小和卷吸口的大小(图3)。喷嘴口径越大,流速越低,卷吸空气越少。喷嘴大小一定时,卷吸口越大,卷吸空气越多。图4所示为临床常用的文丘里面罩。
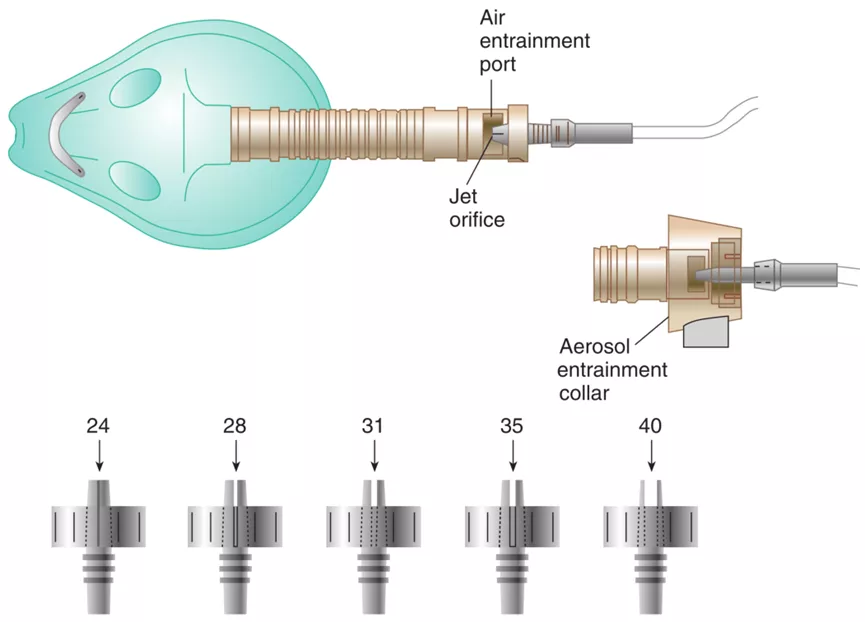
图3 文丘里面罩示意图[5]
如图5,假设忽略氧气的可压缩性和粘性,对A、B两点应用伯努利原理(文丘里效应)进行分析是可行的,可以得出PA>PB。然而A到B点管道的收缩仅是起到加速气流的作用,以便后续卷吸更多空气。此过程中产生的压降不过是流速加快的附带效应,并没有实质性的用途。至于我们所关心的流体从喷嘴射出后,C点的空气为何会被卷吸,PC的大小与流体压力孰大孰小,则无法应用伯努利原理解释,因为C点是流体外的一点,与A、B点均不在同一条流线上,根本不满足伯努利原理的适用条件。
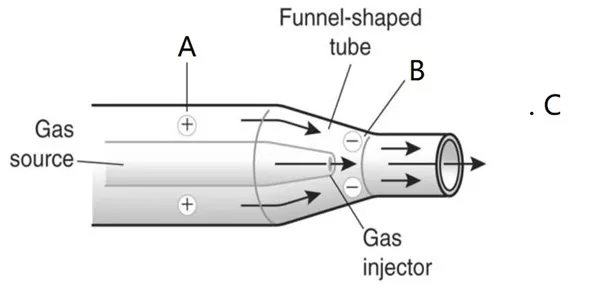
图5 文丘里氧疗装置喷嘴示意图
事实上,稳定状态的无粘射流的静压总是与环境压强相同[6](图6)。当空气没有粘性时,射流的侧面和静止的环境空气之间存在明确的分界。如果射流的静压是大于环境压强的,在这个边界上力不平衡,射流就会向外扩张。在远下游,射流也会由于比环境压强高而沿流向扩张,或叫加速。由伯努利原理,流速增加使流体的静压下降,于是射流的静压一直降到等于环境压强为止。如果射流的静压是小于环境压强的,使用相同思路分析即可得出结论。
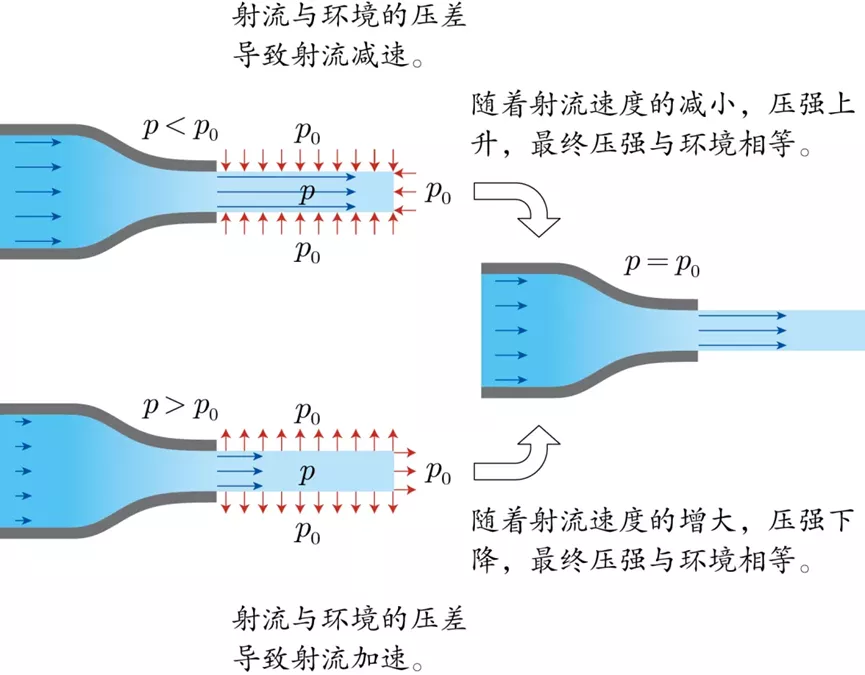
图6 稳定状态的无粘射流的静压与环境相同
物理学实验也证明了这一点。2007年,美国意隆大学(Elon University)的Martin Kamela发文批评物理学教学过程中大量的对于伯努利原理的错误演示,并通过实验演示来说明平直表面的切向流动并不会导致表面压强的下降[7]。如图7所示,当稳定的水平射流经过平直表面时,一端连接至平直表面的U形管内液面并未发生移动,说明没有明显的压强减小现象。
图7 验证射流表面静压的实验装置那么,到底是什么原因导致了文丘里面罩的空气卷吸呢?真正的原因,恰恰在于伯努利原理中忽略掉的粘度[6]。气体是有粘性的,所以会产生摩擦力,在射流中这种摩擦力主要体现在射流的侧面会带动环境的流体,当环境流体被带走一部分,当地压强必然降低,于是周围的流体会源源不断地补充过来(图8)。在文丘里面罩中表现为空气被卷吸进主气流中,从而实现气体总流量的增加和氧浓度的下降。
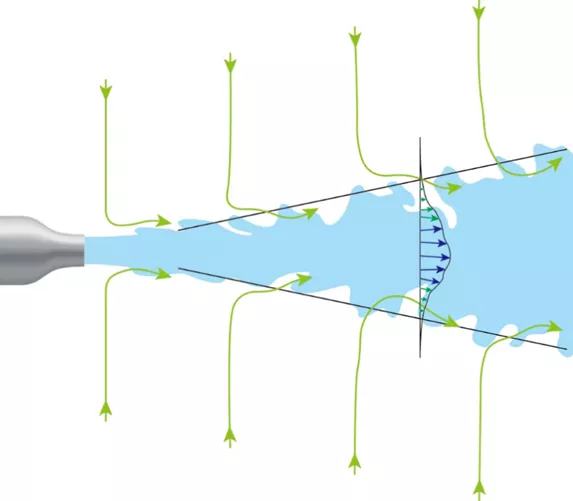
图8 有粘射流的空气卷吸作用
需要强调的是,射流表面压降的程度是非常微弱的。环境流体朝射流流动的最大速度是在接近射流时,此时垂直于射流的速度只是射流的3%左右。假设射流速度是10 m/s,产生的负压是:
可以看出这个负压非常小,这也是图7所示的实验装置未显示出明显压降的原因。因此,不能认为是压降的产生将环境流体“吸入”了射流,而是由于粘性的作用使射流先带走了环境流体才产生了压降,压降又起到补充“新鲜”环境流体的作用。流体力学中的另一种效应——科恩达效应(Coandă effect)与这种空气卷吸作用的原理类似。科恩达效应也叫康达效应,它以罗马尼亚发明家Henri Coandă的名字命名,指有粘度的流体流经一个壁面时,产生一种“附壁”效应,使流体发生弯折,沿着壁面转向的现象(图9)。
如前所述,射流产生的压降很低,按理说不足以将射流“吸向”壁面,产生明显的科恩达效应。但是,一旦有壁面存在时,这个负压是会成倍增加的(图10)。当射流的一侧有壁面时,受壁面的阻碍,射流带走部分空气后,原来的地方得不到足够的空气补充,当地的压强就会降低,气流则由于两侧的压力不均衡而被压向壁面。或者说,被射流带走的空气更多地靠射流自身来补充了[8]。
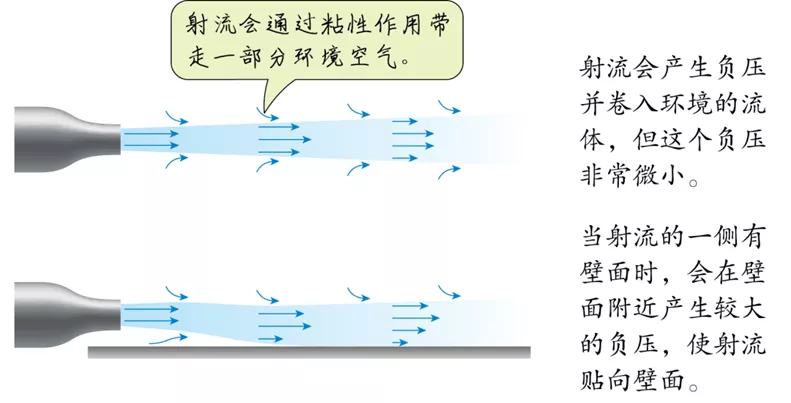
图10 射流产生科恩达效应的原理
当您打开浏览器或短视频APP,搜索“伯努利”得到的10个伯努利原理在生活中的“妙用”中,可能有9个是对伯努利原理的错误解读,包括但不限于向两张纸中间吹气两张纸贴在一起、列车站台安全线、船吸现象、香蕉球和飞机升力的原理等[9-12]。当了解了伯努利原理的适用条件后,便能很容易识破其中的破绽。
伯努利原理(文丘里效应)有严苛的适用条件,并不能用于解释文丘里面罩空气卷吸作用的产生原理。与产生科恩达效应的原理类似,流体的粘性是文丘里面罩产生空气卷吸作用的根本原因。
[1]CAMPBELL E. A method of controlled oxygen administration which reduces the risk of carbon-dioxide retention [J]. The Lancet, 1960, 276(7140):12-14.
[2]SCACCI R. Air entrainment masks: jet mixing is how they work; the Bernoulli and Venturi principles are how they don't [J]. 1979.
[3]KITTREDGE P. Neither Venturi nor Bernoulli [J]. The Lancet, 1983, 321(8317):182.
[4]平中物创工作室. 伯努利效应和康达效应[EB/OL]. (2020). https://mp.weixin.qq.com/s/k6lzm7Ob8Sl5_z2wlL44Ew
[5]KACMAREK R M, STOLLER J K, HEUER A J, et al. Egan's Fundamentals of Respiratory Care [M]. Elsevier, 2017.
[6]王洪伟. 射流的压强与环境相等[EB/OL].(2020). https://mp.weixin.qq.com/s/jymgThhTucIuNdaCsg3fsA
[7]KAMELA M. Thinking about bernoulli [J]. The Physics Teacher, 2007, 45(6):379-381.
[8]王洪伟. 流体科恩达效应[EB/OL].(2021). https://mp.weixin.qq.com/s/Pz_KeNcXvq6ZfUV2aghMTA
[9]王洪伟. 你会吹纸条吗?[EB/OL].(2020). https://mp.weixin.qq.com/s/1kIq51CgwAZ56Tbb17fapg
[10]王洪伟. 列车会“吸人”吗?[EB/OL].(2020). https://mp.weixin.qq.com/s/7f3mBtYSPtxOaGwbPsGlrg
[11]王洪伟. 弧线球的原理[EB/OL].(2020). https://mp.weixin.qq.com/s/YoCrH117Ud3rOQAwZkrqeQ
[12]王洪伟. 升力的原理[EB/OL].(2020). https://mp.weixin.qq.com/s/LNxqqPZz5wsTn9-GPVAAuA

陶程
 后可发表评论
后可发表评论




 公众号
公众号
 客服微信
客服微信